libE57 Coordinate systems

This is a list of the coordinate systems used in the E2807 standard and the libE57 library.

THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE, TITLE AND NON-INFRINGEMENT. IN NO EVENT SHALL THE COPYRIGHT HOLDERS OR ANYONE DISTRIBUTING THE SOFTWARE BE LIABLE FOR ANY DAMAGES OR OTHER LIABILITY, WHETHER IN CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.

Click each item to expand its details.

• XYZ - Cartesian Coordinates

X, Y, Z - Points in cartesian coordinates are represented by an ordered triple (x, y, z) where x, y and z are coordinates along the X, Y, Z axis, respectively. The Z-axis is in the UP direction, the Y-axis is the northing and X-axis is the easting. The coordinate system is right-handed and is measured in meters. If a lidar scanner uses a left-handed system, the data should be converted into this right-handed definition.



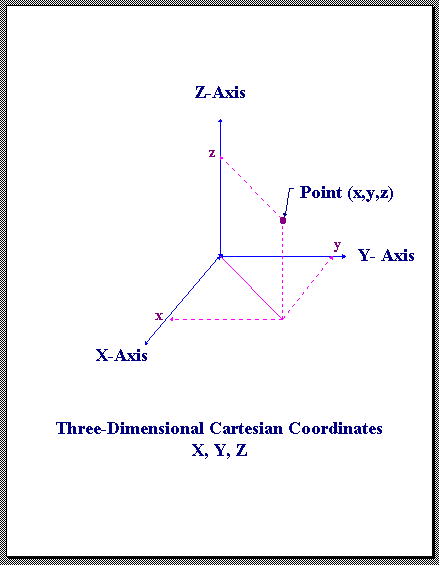
X,Y,Z Cartesian Coordinates

• CYL - Cylindrical Coordinates

Radial (ρ), Azimuth (θ), Z - Points in cylindrical coordinates are represented by an ordered triplet (ρ,θ,z), where ρ is the radial distance (in meters), θ is the azimuth angle (in radians), and z is the height (in meters).

The following restrictions on cylindrical coordinates are applied:

ρ >= 0

-π < θ <= π



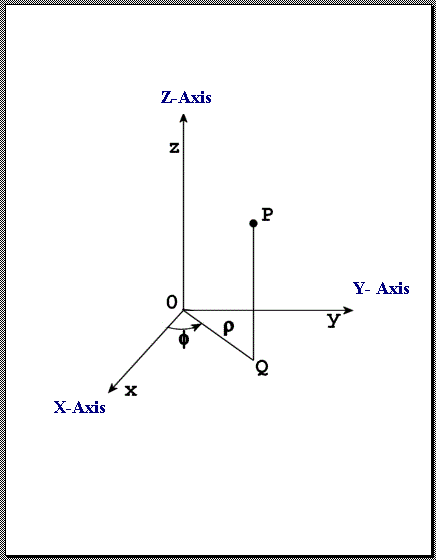
Radial, Azimuth, and Z Coordinates

• RAE - Spherical Coordinates

Range (r), Azimuth (θ), Elevation (φ) - Points in spherical coordinates are represented by an ordered triplet ( r, θ, φ), where r is the range (in meters), θ is the azimuth angle (in radians), and φ is the elevation angle (in radians). The azimuth angle is measured as the counterclock-wise rotation of the positive X-axis about the positive Z-axis of a Cartesian reference frame.

The following restrictions on spherical coordinates are applied:

r >= 0

-π < θ <= π

-π/2 <= φ <= π/2



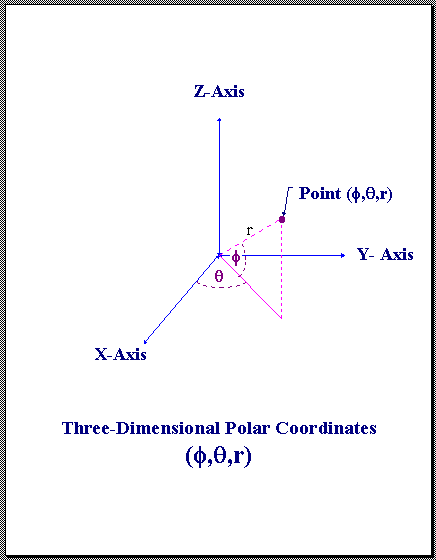
Range, Azimuth, and Elevation Coordinates

• Conversion between XYZ and CYL Coordinates

The conversion between cylindrical and cartesian coordinates are accomplished through the formulas:

x = ρ cos( θ )

y = ρ sin( θ )

z = z

ρ = √ x² + y²

θ = arctan2( y, x )

z = z

• Conversion between XYZ and RAE Coordinates

The conversion between spherical and cartesian coordinates are accomplished through the formulas:

x = r cos( φ ) cos( θ )

y = r cos( φ ) sin( θ )

z = r sin( φ )

r = √ x² + y² + z²

θ = arctan2( y, x )

φ = arcsin( z / r )

• Scanner Coordinate System

The Scanner's coordinate system is defined by the manufacturer of the scanner. The Pose/Translation vector is the position of the scanner's nodal point (origin) in the World Coordinate System of the E57 file.



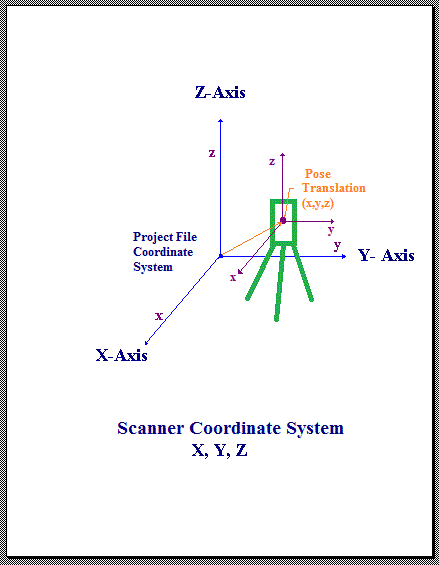
Scanner Coordinate System

• Pinhole Camera Projection Model

Pinhole representation stores an image that is mapped from 3D using a pinhole projection model. Digital cameras with typical, non-fisheye, lenses are well-approximated by this model.

Given a point (x, y, z) in cartesian coordinates in the camera frame of reference, where z < 0, the image coordinates (Ximage, Yimage) are given by the following equations of projection:

Ximage = principalPointX - ( x / z) (focalLength / pixelWidth)

Yimage = principalPointY - ( y / z) (focalLength / pixelHeight)



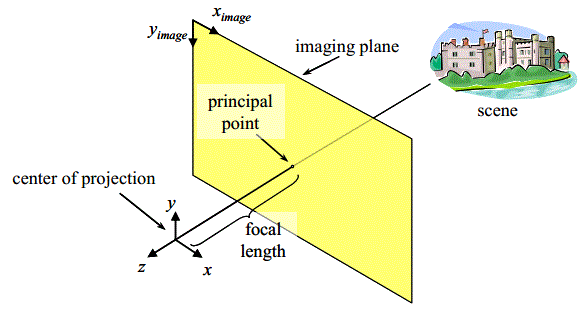
Pinhole Camera Projection Model

The model allows 3D points to be projected onto camera images and image pixels to be projected into 3D space.

• Spherical Camera Projection Model

Spherical representation stores an image that is mapped from 3D using a spherical projection model. Image from fisheye lenses or image mosaics generated from a single position can be represented using this model.

Given a point in spherical coordinates (r, θ, φ), the image coordinates (Ximage, Yimage) are given by the following equations of projection:

Ximage = imageWidth / 2 - θ / pixelWidth

Yimage = imageHeight / 2 - φ / pixelHeight

Image coordinate (0,0) is the top, left corner of the pixel at the top, left corner of the image.



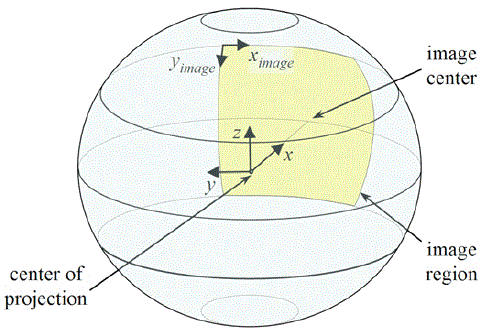
Spherical Camera Projection Model

• Cylindrical Camera Projection Model

Cylindrical representation stores an image that is mapped from 3D using a cylindrical projection model. Images from a rotating single line scanning camera can be represented using this model.

Given a point in cylindrical coordinates (ρ, θ, z), the image coordinates (Ximage, Yimage) are given by the following equations of projection:

Ximage = imageWidth / 2 - θ / pixelWidth

Yimage = principalPointY - z (radius / pixelHeight) / ρ



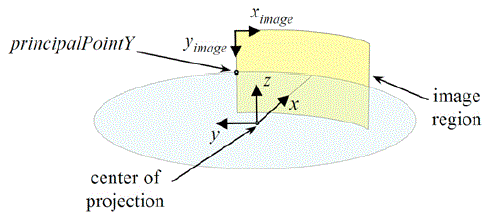
Cylindrical Camera Projection Model

This site is © Copyright 2010 E57.04 3D Imaging System File Format Committee, All Rights Reserved